Introduction
Before I started writing this article, the first thing I did was to google the name of my protein “NendoU” and was greeted by Figure 1. Needless to say, this is not what I was expecting. So, if you’re an anime fan looking for Riki Nendou, a dutiful yet dull-witted boy who likes helping people, particularly prioritising the weak, from The Disastrous Life of Saiki K: I’m afraid you have come to the wrong place. However, now that you’re here, maybe you’d like to learn about an interesting protein involved in SARS-CoV-2 viral replication? It can bind to and process six RNA molecules at a time! Six!
After that interlude, I should get this blog post back on track! So… viruses and proteins. SARS-CoV-2 is an enveloped coronavirus with a non-segmented positive-sense RNA genome, in English this means the RNA genome in SARS-COV-2 can be used “as is” to make viral proteins without prior modification. SARS-CoV-2 has one of the largest RNA genomes among RNA viruses, made up of a replicase gene encoding non-structural proteins (nsps), as well as various structural and accessory genes. During viral replication, depending on the starting point (a.k.a. a ribosomal frame shift), the replicase gene can produce one of two poly-protein chains, which are then cleaved to produce 15-16 individual viral nsps (non-structural Proteins). These nsps then form a large membrane-bound replicase complex with multiple enzymatic activities, like a tiny viral Voltron.
What’s in a Name?
This blog post will focus on SARS-CoV-2 Nsp15, a nidoviral RNA uridylate‐specific endoribonuclease (NendoU). That is a very long and complicated name which conveys a lot of information, so let’s break it down into its individual parts, like when Voltron separates to become several small robots. It’s possible I’ve watched too many cartoons during lockdown:
- Nidoviral – An order of RNA viruses which infect vertebrates and invertebrates.
- RNA – Genetic material used to produce proteins
- Uridylate-specific – Cuts Uridine (U) in RNA, not Cytosine (C), Adenine (A) or Guanine (G)
- Endo – A Greek word meaning inside or within
- Ribonuclease – An enzyme that cuts RNA into smaller pieces.
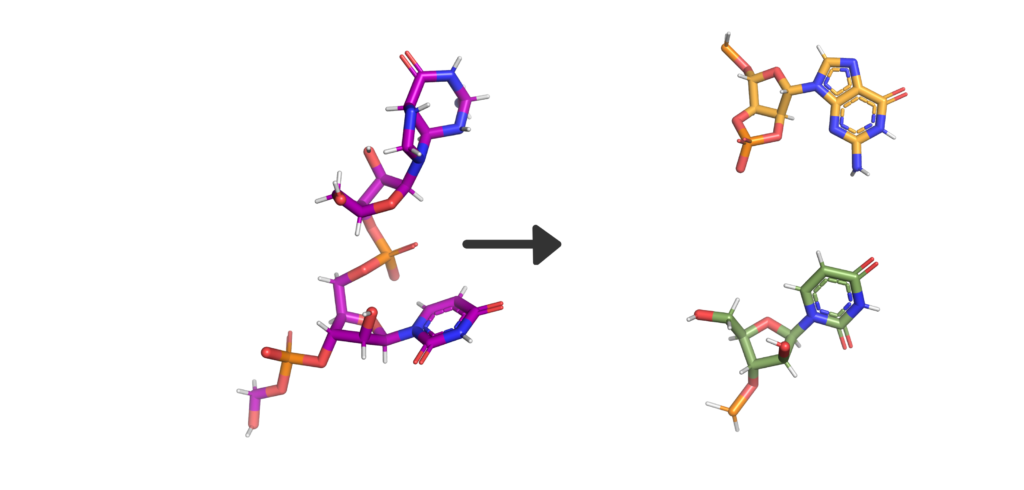
So, what’s in a name? Well, Nsp15 is a viral enzyme that likes to cut at uridine (a building block of RNA) in the middle of an RNA sequence. Quite a lot really. The final bit of the name “NendoU” goes into even more specifics on our protein, as it defines a common family of proteins which share certain traits. The first is that when Nsp15 cuts RNA, it gives a 2′‐3′ cyclic phosphodiester and 5′‐hydroxyl terminus. If we look at Figure 2, you’ll see a purple RNA chain made of two bases linked by an orange phosphate in the middle. When RNA is cleaved by Nsp15, a 2′‐3′ cyclic phosphodiester is made: in the two resulting molecules, the phosphate ion has been incorporated into a 5-membered ring (orange), and the other half of the RNA has a 5′‐hydroxyl, or and OH- group on another 5-membered ring (green). The second thing being a member of the NendoU family tells us is that the catalytic domain of the protein (the business end) is found on the C-terminal end of the protein (the latter half) as this is a shared trait within the NendoU family.
Domains
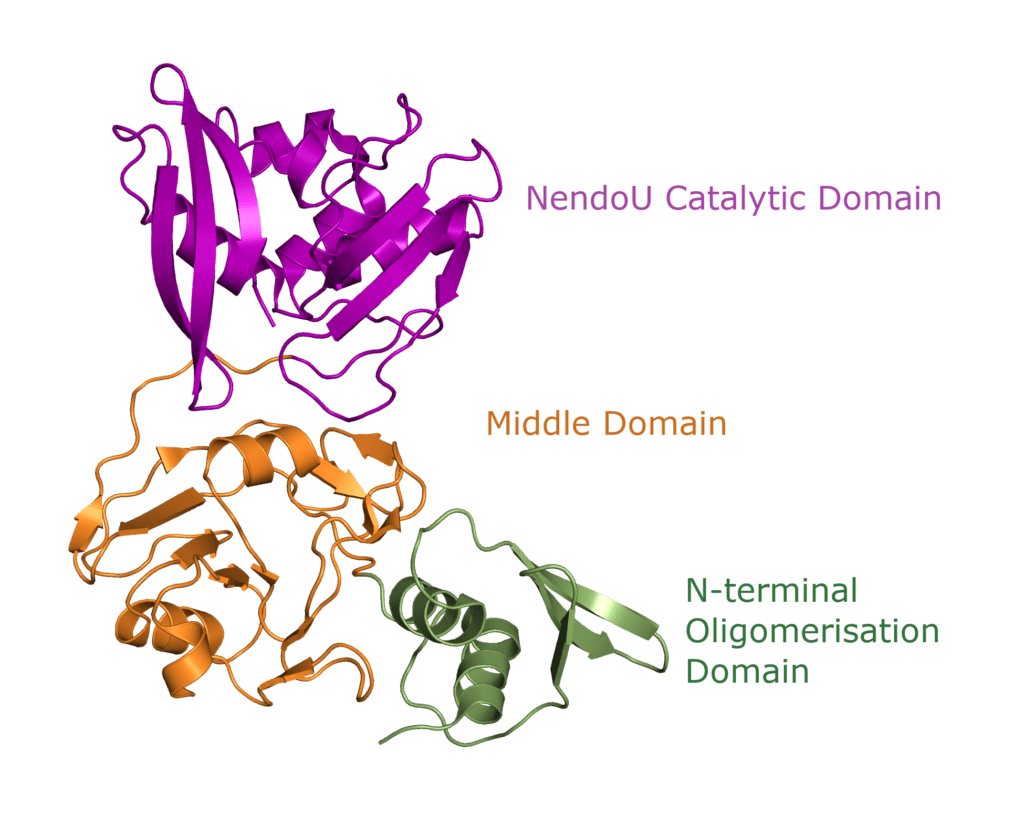
One Nsp15 monomer is made up of three distinct domains, the aforementioned N-terminal oligomerisation domain (green), a middle domain in… well, the middle (orange), and the catalytic NendoU domain at the C-terminal (purple, Figure 3b). Overall SARS-CoV-2 Nsp15 shows high sequence identity with SARS-CoV Nsp15 (88%) and, somewhat lower identity with MERS-CoV (51%) (Youngchang 2020), but the overall structural similarity is very high between the three viruses. For a more detailed breakdown of the secondary structure that makes up individual Nsp15 domains, check out our proteopedia entry!
Tertiary Structure
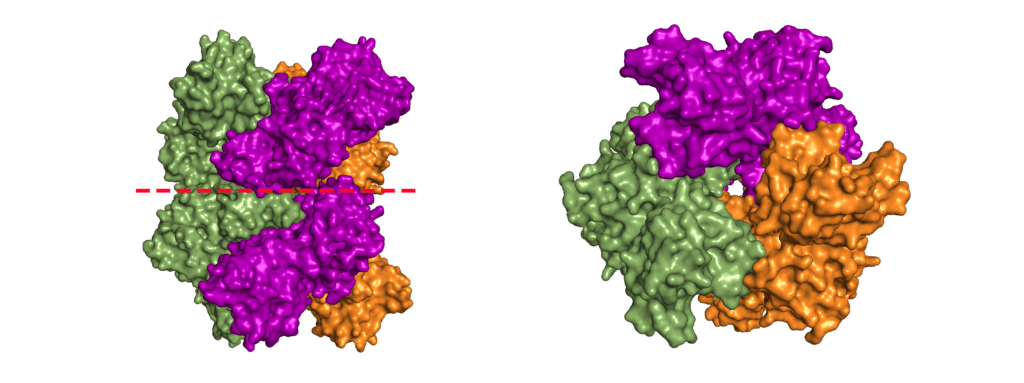
Nsp15 forms a double-ring hexamer made up of a dimer of trimers stabilised by an N-terminal oligomerisation domain. So, three monomers form a trimer which then binds another trimer of monomers. However, If you open a crystal structures this can be confusing as you might not be presented with the whole complex. A crystal is composed of an infinite array of identical (or near enough) molecules related to each other by symmetry. To eliminate the need to store an infinite number of atoms on your computer the PDB file gives you just enough of the crystal to define the unique part. You are then expected to remember that the rest are generated by symmetry. This subset is called the asymmetric unit. Should you want to try and generate the whole crystal you can try, but your computer will likely grind to a halt on its way to infinity (and beyond).
For most structures the asymmetric unit is the interesting part. Often, when the biologically relevant complex has symmetry itself, like Nsp15 does, only part of the complex will be present in the file from the PDB. In the case of the PDB model 6X4I the molecules of each trimer obey the crystal’s three-fold symmetry. The file you download contains two molecules, one monomer from each trimer, and you must generate the symmetry related molecules (shown in green and orange in figure 3) to build the entire complex. These six monomers all come together to form the active enzyme, a 100 Å long and 10-15 Å wide channel, open to solvent from the top, bottom, and three separate side openings in the middle of the hexamer (Figure 4). Formation of the hexamer has been shown to be essential for enzymatic activity, making the oligomerisation interfaces a potential target for structure-based drug design. I’m not sure if I should be proud or disappointed that I didn’t mention Voltron once back there.
The Active Site
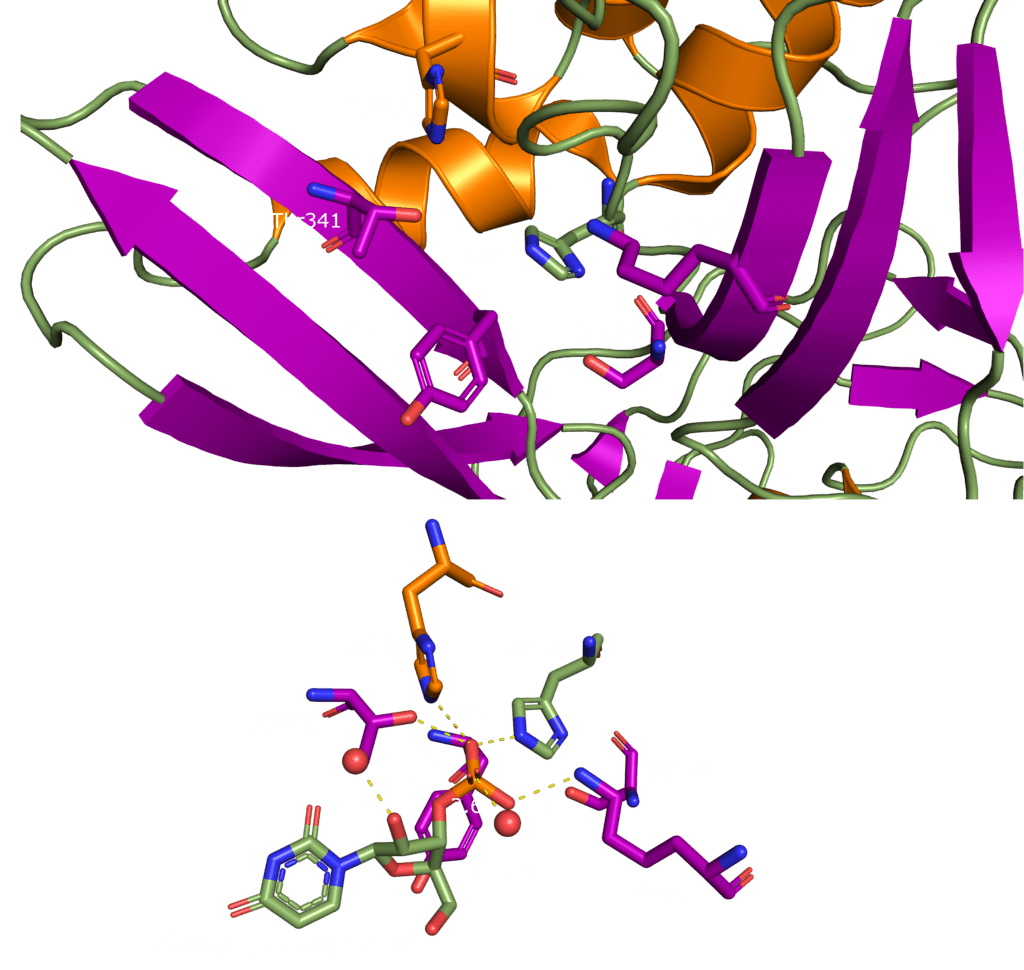
SARS-CoV-2 Nsp15 is a Mn2+ dependent endoribonuclease, meaning it relies on the coordination of manganese to perform the transesterification reaction (cutting RNA). Unfortunately, the structure of SARS-CoV-2 Nsp15 has not been solved with manganese present, but we do have a structure with 3’ uridine monophosphate in the active site (PDBID: 6X4I). It has been proposed that the presence of manganese help stabilise the active site and substrate, but it is yet to been seen. Based on sequence alignment against related enzymes from other viruses we know the active site is made up of six conserved residues that sit in a shallow groove between two β-sheets (His235, His250, Lys290, Thr341, Tyr343, and Ser294), as shown in Figure 5. His235, His250, and Lys290 are predicted to act as a catalytic triad, His235 as a general acid, and His250 as a base with Lys290 governing U specificity.
But What Does it do?
After all that we have a pretty clear picture of what Nsp15 NendoU looks like, but what does it actually do? The fact that it cuts RNA would immediately suggest a role in viral replication, but Nsp15 deficient coronaviruses are still able to replicate. So maybe not, at least it's not essential for replication. Another suggestion is that Nsp15 is involved in interfering with the hosts innate immune response, but other studies suggest this is independent of Nsp15 activity. Finally, it has been suggested that Nsp15 degrades viral RNA as a means of hiding viral infection from the host immune system. So why does coronavirus bother with Nsp15? I’m afraid we don’t exactly know yet, but we’re working on it.
With that I’m going to leave you with one final Voltron reference for making it to the end. Good job, you earned this.

